Incompatibility of quantum measurements

Stern–Gerlach experiment: Silver atoms travelling through an inhomogeneous magnetic field, and being deflected up or down depending on their spin; (1) furnace, (2) beam of silver atoms, (3) inhomogeneous magnetic field, (4) classically expected result, (5) observed result.

Incompatibility of quantum measurements is a crucial concept of quantum information, addressing whether two or more quantum measurements can be performed on a quantum system simultaneously. It highlights the unique and non-classical behavior of quantum systems. This concept is fundamental to the nature of quantum mechanics and has practical applications in various quantum information processing tasks like quantum key distribution and quantum metrology.

History

Early ages

The concept of incompatibility of quantum measurements originated from Heisenberg's uncertainty principle, which states that certain pairs of physical quantities, like position and momentum, cannot be simultaneously measured with arbitrary precision. This principle laid the groundwork for understanding the limitations of measurements in quantum mechanics.

Mid-20th century

In the mid-20th century, researchers began to formalize the idea of compatibility of quantum measurements, and to explore conditions under which a set of measurements can be performed together on a single quantum system without disturbing each other. This was crucial for understanding how quantum systems behave under simultaneous observations.

Late-20th century

The study of incompatibility of quantum measurements gained significant attention with the rise of quantum information theory. Researchers realized that measurement incompatibility is not just a limitation but also a resource for various quantum information processing tasks. For example, it plays a crucial role in quantum cryptography, where the security of quantum key distribution protocols relies on the incompatibility of certain quantum measurements.

21th century

Modern research focuses on quantifying measurement incompatibility using various measures. Quite a number of approaches involve robustness-based measures, which assess how much noise can be added to a set of quantum measurements before they become compatible.

Definition

In quantum mechanics, two measurements, $M_{1}$ and $M_{2}$, are called compatible if and only if there exists a third measurement $M$ of which $M_{1},M_{2}$ can be obtained as margins, or equivalently, from which $M_{1},M_{2}$ can be simulated via classical post-processings. More precisely, let $M_{1}:{\mathcal {A}}_{1}\to {\mathcal {B}}(\mathbb {H} )$ and $M_{2}:{\mathcal {A}}_{2}\to {\mathcal {B}}(\mathbb {H} )$ be two positive operator-valued measures (POVMs), where $(X_{1},{\mathcal {A}}_{1}),(X_{2},{\mathcal {A}}_{2})$ are two measurable spaces, and ${\mathcal {B}}(\mathbb {H} )$ is the set of bounded linear operators on a Hilbert space $\mathbb {H}$. Then $M_{1},M_{2}$ are called compatible (jointly measurable) if and only if there is a POVM $M:{\mathcal {A}}_{1}\otimes {\mathcal {A}}_{2}\to {\mathcal {B}}(\mathbb {H} )$ such that

$M(A_{1}\times X_{2})=M_{1}(A_{1}),$

$M(X_{1}\times A_{2})=M_{2}(A_{2}),$

for all $A_{1}\in {\mathcal {A}}_{1}$ and $A_{2}\in {\mathcal {A}}_{2}$. Otherwise, $M_{1},M_{2}$ are called incompatible. The definition of compatibility of a finite number of POVMs is similar.

An example

Bloch sphere.

For a two-outcome POVM $M_{\pm }$ on a qubit it is possible to write

$M_{\pm }={\cfrac {1}{2}}\left[(1\pm \alpha )\mathbf {I} \pm {\vec {m}}\cdot {\vec {\sigma }}\right],$

where ${\vec {m}}\cdot {\vec {\sigma }}=m_{x}\sigma _{x}+m_{y}\sigma _{y}+m_{z}\sigma _{z}$ with $\sigma _{x},\sigma _{y},\sigma _{z}$ are Pauli matrices. Let $M_{\pm |1}$ and $M_{\pm |2}$ be two such POVMs with $\alpha _{1}=\alpha _{2}=0$, ${\vec {m}}_{1}=(\mu ,0,0)$, and ${\vec {m}}_{2}=(0,0,\mu )$, where $\mu \in [0,1]$. Then for $\mu \in [0,1/{\sqrt {2}}]$ one can verify that the following POVM

$M_{+,+}:={\cfrac {1}{4}}\left[\mathbf {I} +\mu (\sigma _{x}+\sigma _{z})\right],$

$M_{-,+}:={\cfrac {1}{4}}\left[\mathbf {I} +\mu (-\sigma _{x}+\sigma _{z})\right],$

$M_{+,-}:={\cfrac {1}{4}}\left[\mathbf {I} +\mu (\sigma _{x}-\sigma _{z})\right],$

$M_{-,-}:={\cfrac {1}{4}}\left[\mathbf {I} +\mu (-\sigma _{x}-\sigma _{z})\right],$

is a compatiblizer of $M_{\pm |1}$ and $M_{\pm |2}$, despite the fact that $M_{\pm |1}$ and $M_{\pm |2}$ are noncommutative for $\mu \in (0,1/{\sqrt {2}}]$. As for $\mu \in (1/{\sqrt {2}},1]$, it was shown that $M_{\pm |1},M_{\pm |2}$ are incompatible.

Criteria for compatibility

Analytical criteria

Let $M_{1},M_{2}$ be two two-outcome POVMs on a qubit. It was shown that $M_{1},M_{2}$ are compatible if and only if

$(1-C_{1}^{2}-C_{2}^{2})\left(1-{\cfrac {\alpha _{1}^{2}}{C_{1}^{2}}}-{\cfrac {\alpha _{2}^{2}}{C_{2}^{2}}}\right)\leqslant \left({\vec {m}}_{1}\cdot {\vec {m}}_{2}-\alpha _{1}\alpha _{2}\right)^{2},$

where $C_{i}={\cfrac {1}{2}}\left[{\sqrt {(1+\alpha _{i})^{2}-\left|{\vec {m}}_{i}\right|^{2}}}+{\sqrt {(1-\alpha _{i})^{2}-\left|{\vec {m}}_{i}\right|^{2}}}\right],$ for $i=1,2$. Moreover, let $M_{1},M_{2},M_{3}$ be three two-outcome POVMs on a qubit with $\alpha _{1}=\alpha _{2}=\alpha _{3}=0$. Then it was proved that $M_{1},M_{2},M_{3}$ are compatible if and only if

$\min _{{\vec {n}}\in \mathbb {R} ^{3}}\sum _{j=0}^{3}\left|{\vec {n}}_{j}-{\vec {n}}\right|\leqslant 4,$

where ${\vec {n}}_{0}={\vec {m}}_{1}+{\vec {m}}_{2}+{\vec {m}}_{3}$, and ${\vec {n}}_{j}=2{\vec {m}}_{j}-{\vec {n}}_{0}$ for $j=1,2,3$.

Numerical criteria

For a finite number of POVMs $\{M_{x|i}\}$ on a finite-dimensional quantum system, with a finite number of measurement outcomes (labeled by $x$), one can cast the following semidefinite program (SDP) to decide whether they are compatible or not:

$\mathrm {given} \ \{M_{x|i}\},\{p(x|i,\lambda )\}$

$\max _{\{G_{\lambda }\}}\mu$

$\mathrm {subject\ to} \sum _{\lambda }p(x|i,\lambda )G_{\lambda }=M_{x|i},\quad \forall x,i,$

$G_{\lambda }\geqslant \mu \mathbf {I} ,\quad \forall \lambda \quad \mathrm {and} \quad \sum _{\lambda }G_{\lambda }=\mathbf {I} .$

where $\{p(x|i,\lambda )\}$ is a deterministic classical post-processing (i.e., $0$ or $1$ valued conditional probability density). If for all $\{p(x|i,\lambda )\}$ the maximizer $\{G_{\lambda }\}$ leads to a negative $\mu$, then $\{M_{x|i}\}$ are incompatible. Otherwise, they are compatible.

Quantifiers of incompatibility

Incompatibility noise robustness

Let $\{M_{x|i}\}$ be a finite number of POVMs. Incompatibility noise robustness $R_{\mathrm {n} }$ of $\{M_{x|i}\}$ is defined by

$R_{\mathrm {n} }(\{M_{x|i}\})=\inf\{p\in [0,1]|\{(1-p)M_{x|i}+p\mathrm {I} /|x|\}\ \ {\text{are compatible}}\},$

where $|x|$ denotes the number of outcomes. This quantity is a monotone under quantum channels since (i) it vanishes on $\{M_{x|i}\}$ that are compatible, (ii) it is symmetric under the exchange of POVMs, and (iii) it does not increase under the pre-processing by a quantum channel.

Incompatibility weight

Incompatibility weight $W$ of POVMs $\{M_{x|i}\}$ is defined by

$W(\{M_{x|i}\})=\inf \left\{q\geqslant 0:\left\{{\cfrac {M_{x|i}-qN_{x|i}}{1-q}}\right\}\ \ {\text{are compatible}}\right\},$

where $\{N_{x|i}\}$ is any set of POVMs. This quantity is a monotone under compatibility nondecreasing operations that consist of pre-processing by a quantum instrument and classical post-processing.

Incompatibility robustness

Incompatibility robustness $R$ of POVMs $\{M_{x|i}\}$ is defined by

$R(\{M_{x|i}\})=\inf \left\{r\geqslant 0:\left\{{\cfrac {M_{x|i}+rN_{x|i}}{1+r}}\right\}\ \ {\text{are compatible}}\right\},$

where $\{N_{x|i}\}$ is any set of POVMs. Similar to incompatibility weight, this quantity is a monotone under compatibility nondecreasing operations.

All these quantifiers are based on the convex distance of incompatible POVMs to the set of compatible ones under the addition of different types of noise. Specifically, all these quantifiers can be evaluated numerically, as they fall under the framework of SDPs. For instance, it was shown that incompatibility robustness can be cast as the following SDP:

$\mathrm {given} \ \{M_{x|i}\}$

$\min _{\left(\{G_{\lambda }\},\{p(x|i,\lambda )\}\right)}{\cfrac {1}{d}}\sum _{\lambda }\mathrm {tr} (G_{\lambda })$

$\mathrm {subject\ to} \sum _{\lambda }p(x|i,\lambda )G_{\lambda }\geqslant M_{x|i},\quad \forall x,i,$

$G_{\lambda }\geqslant 0,\quad \forall \lambda \quad \mathrm {and} \quad \sum _{\lambda }G_{\lambda }={\cfrac {\mathbf {I} }{d}}\left[\sum _{\lambda }\mathrm {tr} (G_{\lambda })\right],$

where $\{p(x|i,\lambda )\}$ is a deterministic classical post-processing, and $d$ is the dimension of the Hilbert space on which $\{M_{x|i}\}$ are performed. If the minimizer is $\left(\{G_{\lambda }'\},\{p(x|i,\lambda )'\}\right)$, then $R(\{M_{x|i}\})={\cfrac {1}{d}}\sum _{\lambda }\mathrm {tr} (G_{\lambda }')-1$.

Incompatibility and quantum information processing

Measurement incompatibility is intrinsically tied to the nonclassical features of quantum correlations. In fact, in many scenarios, it becomes evident that incompatible measurements are necessary to exhibit nonclassical correlations. Since such correlations are essential for tasks like quantum key distribution or quantum metrology, these connections underscore the resource aspect of measurement incompatibility.

Bell nonlocality

Scheme of a "two-channel" Bell test.
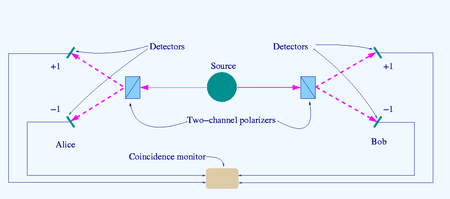
The source produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.

Bell nonlocality is a phenomenon where the correlations between quantum measurements on entangled quantum states cannot be explained by any local hidden variable theory. This was first demonstrated by Bell through Bell's Theorem, which showed that certain predictions of quantum mechanics are incompatible with the principle of locality (an idea that objects are only directly influenced by their immediate surroundings).

If the POVMs on Alice's side are compatible, then they will never lead to Bell nonlocality. However, the converse is not true. It was shown that there exist three binary measurements on a qubit, pairwise compatible but globally incompatible, yet not leading to any Bell nonlocality .

Quantum steering

Quantum steering is a phenomenon where one party (Alice) can influence the state of a distant party's (Bob's) quantum system through local measurements on her own quantum system. This was first introduced by Schrödinger and is a form of quantum nonlocality. It demonstrates that the state of Bob's quantum system can be "steered" into different states depending on the local measurements performed by Alice.

For quantum steering to occur, the local measurements performed by Alice must be incompatible. This is because steering relies on the ability to create different outcomes in Bob's system based on Alice's measurements, which is only possible if those measurements are not compatible. Further, it was shown that if the following POVMs $\left\{\sigma _{i}^{-1/2}\sigma _{x|i}\sigma _{i}^{-1/2}\right\}$ are incompatible, then a state assemblage $\{\sigma _{x|i}\}$ is steerable, where $\sigma _{i}=\sum _{x}\sigma _{x|i}$.

Quantum contextuality

Quantum contextuality refers to the idea that the outcome of a quantum measurement cannot be explained by any pre-existing value that is independent of the measurement context. In other words, the result of a quantum measurement depends on which other measurements are being performed simultaneously. This concept challenges classical notions of reality, where it is assumed that properties of a system exist independently of measurement.

It was proved that any set of compatible POVMs leads to preparation noncontextual correlations for all input quantum states. Conversely, the existence of a preparation noncontextual model for all input states implies compatibility of the involved POVMs.

See also

• Generalized probabilistic theory
• Mathematical formulation of quantum mechanics
• POVM
• Qudit
• Quantum information

Further reading

• Alter, Orly; Yamamoto, Yoshihisa (2001). Quantum Measurement of a Single System. New York: Wiley. doi:10.1002/9783527617128. ISBN 9780471283089.
• Busch, Paul; Lahti, Pekka; Pellonpää, Juha-Pekka; Ylinen, Kari (2016). Quantum measurement. Vol. 23. Springer. pp. 261–262. Bibcode:2016qume.book.....B. doi:10.1007/978-3-319-43389-9. ISBN 978-3-319-43387-5.
• Braginsky, Vladimir B.; Khalili, Farid Ya. (1992). Quantum Measurement. Cambridge University Press. ISBN 978-0-521-41928-4.
• Greenstein, George S.; Zajonc, Arthur G. (2006). The Quantum Challenge: Modern Research On The Foundations Of Quantum Mechanics (2nd ed.). Jones & Bartlett Learning. ISBN 978-0763724702.
• Jordan, Andrew N.; Siddiqi, Irfan A. (2024). Quantum Measurement: Theory and Practice. Cambridge University Press. ISBN 978-1009100069.
• Wheeler, John A.; Zurek, Wojciech H., eds. (1983). Quantum Theory and Measurement. Princeton University Press. ISBN 978-0-691-08316-2.