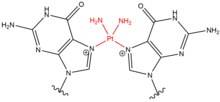
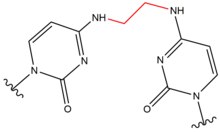
Crosslinking of DNA

In genetics, crosslinking of DNA occurs when various exogenous or endogenous agents react with two nucleotides of DNA, forming a covalent linkage between them. This crosslink can occur within the same strand (intrastrand) or between opposite strands of double-stranded DNA (interstrand). These adducts interfere with cellular metabolism, such as DNA replication and transcription, triggering cell death. These crosslinks can, however, be repaired through excision or recombination pathways.
DNA crosslinking also has useful merit in chemotherapy and targeting cancerous cells for apoptosis,[1] as well as in understanding how proteins interact with DNA.
Crosslinking agents
Many characterized crosslinking agents have two independently reactive groups within the same molecule, each of which is able to bind with a nucleotide residue of DNA. These agents are separated based upon their source of origin and labeled either as exogenous or endogenous. Exogenous crosslinking agents are chemicals and compounds, both natural and synthetic, that stem from environmental exposures such as pharmaceuticals and cigarette smoke or automotive exhaust. Endogenous crosslinking agents are compounds and metabolites that are introduced from cellular or biochemical pathways within a cell or organism.
Exogenous agents
- Nitrogen mustards are exogenous alkylating agents which react with the N7 position of guanine. These compounds have a bis-(2-ethylchloro)amine core structure, with a variable R-group, with the two reactive functional groups serving to alkylate nucleobases and form a crosslink lesion. These agents most preferentially form a 1,3 5'-d(GNC) interstrand crosslink. The introduction of this agent slightly bends the DNA duplex to accommodate for the agent's presence within the helix.[2] These agents are often introduced as a pharmaceutical and are used in cytotoxic chemotherapy.[3]
- Cisplatin (cis-diamminedichloroplatinum(II)) and its derivatives mostly act on adjacent guanines at their N7 positions. The planar compound links to nucleobases through water displacement of one or both of its chloride groups, allowing cisplatin to form monoadducts to DNA or RNA, intrastrand DNA crosslinks, interstrand DNA crosslinks, and DNA-protein crosslinks.[4] When cisplatin generates DNA crosslinks, it more frequently forms 1,2-intrastrand crosslinks (5'-GG), but also forms 1,3-intrastrand crosslinks (5-GNG) at lower percentages.[5][6] When cisplatin forms interstrand crosslinks (5'-GC), there is a severe distortion to the DNA helix due to a shortened distance between guanines on opposite strands and a cytosine that is flipped out of the helix as a consequence of the GG interaction.[7] Similar to nitrogen mustards, cisplatin is used frequently in chemotherapy treatment - especially for testicular and ovarian cancers.[8]
- Chloro ethyl nitroso urea (CENU), specifically carmustine (BCNU), are crosslinking agents that are widely used in chemotherapy, particularly for brain tumors. These agents differ from other crosslinkers as they alkylate O6 of guanine to form an O6-ethanoguanine. This intermediate compound then leads to an interstrand crosslink between a GC basepair. These crosslinking agents only result in small distortions to the DNA helix due to the molecules' smaller size.
- Psoralens are natural compounds (furocoumarins) present in plants. These compounds intercalate into DNA at 5'-AT sequence sites and form thymidine adducts when activated in the presence of Ultra Violet-A (UV-A) rays.[9] These covalent adducts are formed by linking the 3, 4 (pyrone) or 4', 5’ (furan) edge of psoralen to the 5, 6 double bond of thymine. Psoralens can form two types of monoadducts and one diadduct (an interstrand crosslink) with thymine.[10] These adducts result in local distortions to DNA at the site of intercalation. Psoralens are used in the medical treatment of skin diseases, such as psoriasis and vitiligo.
- Mitomycin C (MMC) is from a class of antibiotics that are used broadly in chemotherapy, often with gastrointestinal related cancers. Mitomycin C can only act as a crosslinker when a DNA nucleotide has had a reduction to its quinone ring. When two dG's have been rearranged and methylated in this manner, a 5'-GC interstrand crosslink can be formed with the exo amines of each nucleobase. Mitomycin also harbors the ability to form monoadducts and intrastrand crosslinks with DNA as well. The interstrand crosslinks of Mitomycin C are formed in the minor groove of DNA, inducing a moderate widening or stretching to the DNA helix in order to accommodate for the presence of the molecule within the two strands.
Endogenous agents
- Nitrous acid is formed as a byproduct in the stomach from dietary sources of nitrites and can lead to crosslink lesions in DNA through the conversion of amino groups in DNA to carbonyls. This type of lesion occurs most frequently between two guanosines, with 1 of 4 deaminated guanosines resulting in an interstrand crosslink.[11] It induces formation of interstrand DNA crosslinks at the amino group of exocyclic N2 of guanine at 5'-CG sequences. This lesion mildly distorts the double helix.
- Bifunctional aldehydes are reactive chemicals that are formed endogenously via lipid peroxidation and prostoglandin biosynthesis.[12] They create etheno adducts formed by aldehyde which undergo rearrangements to form crosslinks on opposite strands of DNA. Malondialdehyde is a prototypical example that can crosslink DNA via two exocyclic guanine amino groups.[13] Other aldehydes, such as formaldehyde and acetylaldehyde, can introduce interstrand crosslinks and often act as exogenous agents as they are found in many processed foods. Often found within pesticides, tobacco smoke, and automotive exhaust, α,β unsaturated aldehydes, such as acrolein and crotonaldehyde, are further exogenous agents that may induce DNA crosslinks. Unlike other crosslinking agents, aldehyde-induced crosslinking is an intrinsically reversible process. NMR structure of these types of agents as interstrand crosslinks show that a 5'-GC adduct results in minor distortion to DNA, however a 5'-CG adduct destabilizes the helix and induces a bend and twist in the DNA.[14]
- DNA crosslinking lesions can also be formed when under conditions of oxidative stress, in which free oxygen radicals generate reactive intermediates in DNA, and these lesions have been implicated in aging and cancer. Tandem DNA lesions are formed at a substantial frequency by ionizing radiation and metal-catalyzed H2O2 reactions. Under anoxic conditions, the predominant double-base lesion is a species in which the C8 of guanine is linked to the 5-methyl group of an adjacent 3'-thymine (G[8,5- Me]T), forming intrastrand lesions.[15][16]
Summary table of crosslinking agents
Repair of DNA crosslinks
Crosslinked DNA is repaired in cells by a combination of enzymes and other factors from the nucleotide excision repair (NER) pathway, homologous recombination, and the base excision repair (BER) pathway. To repair interstrand crosslinks in eukaryotes, a 3’ flap endonuclease from the NER, XPF-ERCC1, is recruited to the crosslinked DNA, where it assists in ‘unhooking’ the DNA by cleaving the 3’ strand at the crosslink site. The 5’ strand is then cleaved, either by XPF-ERCC1 or another endonuclease, forming a double-strand break (DSB), which can then be repaired by the homologous recombination pathway.[17]
DNA crosslinks generally cause loss of overlapping sequence information from the two strands of DNA. Therefore, accurate repair of the damage depends on retrieving the lost information from an undamaged homologous chromosome in the same cell. Retrieval can occur by pairing with a sister chromatid produced during a preceding round of replication. In a diploid cell retrieval may also occur by pairing with a non-sister homologous chromosome, as occurs especially during meiosis.[citation needed] Once pairing has occurred, the crosslink can be removed and correct information introduced into the damaged chromosome by homologous recombination.
Cleavage of the bond between a deoxyribose sugar in DNA's sugar-phosphate backbone and its associated nucleobase leaves an abasic site in double stranded DNA. These abasic sites are often generated as an intermediate and then restored in base excision repair. However, if these sites are allowed to persist, they can inhibit DNA replication and transcription.[18] Abasic sites can react with amine groups on proteins to form DNA-protein crosslinks or with exocyclic amines of other nucleobases to form interstrand crosslinks. To prevent interstrand or DNA-protein crosslinks, enzymes from the BER pathway tightly bind the abasic site and sequester it from nearby reactive groups, as demonstrated in human alkyladenine DNA glycosylase (AAG) and E. coli 3-methyladenine DNA glycosylase II (AlkA).[19] in vitro evidence demonstrated that the Interstand Cross-Links induced by abasic site (DOB-ICL) is a replication-blocking and highly miscoding lesion. Compared to several other TLS pols examined, pol η is likely to contribute to the TLS-mediated repair of the DOB-ICL in vivo.[20] By using O6-2'-deoxyguanosine-butylene-O6-2'-deoxyguanosine (O6-dG-C4-O6-dG) DNA lesions which is a chemically stable structure, the bypassing activity of several DNA polymerases had been investigated and the results demonstrated that pol η exhibited the highest bypass activity; however, 70% of the bypass products were mutagenic containing substitutions or deletions. The increase in the size of unhooked repair intermediates elevates the frequency of deletion mutation. [21]
Treatment of E. coli with psoralen-plus-UV light (PUVA) produces interstrand crosslinks in the cells’ DNA. Cole et al.[22] and Sinden and Cole[23] presented evidence that a homologous recombinational repair process requiring the products of genes uvrA, uvrB, and recA can remove these crosslinks in E. coli. This process appears to be quite efficient. Even though one or two unrepaired crosslinks are sufficient to inactivate a cell, a wild-type bacterial cell can repair and therefore recover from 53 to 71 psoralen crosslinks. Eukaryotic yeast cells are also inactivated by one remaining crosslink, but wild type yeast cells can recover from 120 to 200 crosslinks.[24]
Applications
Crosslinking of DNA and protein
Biochemical interaction methods
DNA-protein crosslinking can be caused by a variety of chemical and physical agents, including transition metals, ionizing radiation, and endogenous aldehydes, in addition to chemotherapeutic agents.[25] Similar to DNA crosslinking, DNA-protein crosslinks are lesions in cells that are frequently damaged by UV radiation. The UV's effect can lead to reactive interactions and cause DNA and the proteins that are in contact with it to crosslink. These crosslinks are very bulky and complex lesions. They primarily occur in areas of the chromosomes that are undergoing DNA replication and interfere with cellular processes.
The advancement in structure-identification methods has progressed, and the addition in the ability to measure interactions between DNA and protein is a requirement to fully understand the biochemical processes. The structure of DNA-protein complexes can be mapped by photocrosslinking, which is the photoinduced formation of a covalent bond between two macromolecules or between two different parts of one macromolecule. The methodology involves covalently linking a DNA-binding motif of the target sequence-specific DNA-binding protein with a photoactivatable crosslinking agent capable of reacting with DNA nucleotides when exposed to UV. This method provides information on the interaction between the DNA and protein in the crosslink.[26]
Clinical treatments
DNA repair pathways can result in the formation of tumor cells. Cancer treatments have been engineered using DNA cross-linking agents to interact with nitrogenous bases of DNA to block DNA replication. These cross-linking agents have the ability to act as single-agent therapies by targeting and destroying specific nucleotides in cancerous cells. This result is stopping the cycle and growth of cancer cells; because it inhibits specific DNA repair pathways, this approach has a potential advantage in having fewer side effects.[27]
In humans, the leading cause of cancer deaths worldwide is lung cancer, including non small cell lung carcinoma (NSCLC) which accounts for 85% of all lung cancer cases in the United States.[28] Individuals with NSCLC are often treated with therapeutic platinum compounds (e.g. cisplatin, carboplatin or oxaliplatin) (see Lung cancer chemotherapy) that cause interstrand DNA crosslinks. Among individuals with NSLC, low expression of the breast cancer 1 gene (BRCA1) in the primary tumor has correlated with improved survival after platinum-containing chemotherapy.[29][30] This correlation implies that low BRCA1 in the cancer, and the consequent low level of DNA repair, causes vulnerability of the cancer to treatment by the DNA crosslinking agents. High BRCA1 may protect cancer cells by acting in the homologous recombinational repair pathway that removes the damages in DNA introduced by the platinum drugs. The level of BRCA1 expression is potentially an important tool for tailoring chemotherapy in lung cancer management.[29][30]
Clinical chemotherapeutics can induce enzymatic and non-enzymatic DNA-protein crosslinks. An example of this induction is with platinum derivatives, such as cisplatin and oxaliplatin. They create non-enzymatic DNA-protein crosslinks through non-specific crosslinking of chromatin-interacting proteins to DNA. Crosslinking is also possible in other therapeutic agents by either stabilizing covalent DNA–protein reaction intermediates or by creating a pseudosubstrate, which traps the enzyme on DNA. Camptothecin derivatives, such as irinotecan and topotecan, target and trap specific DNA topoisomerase 1 (TOP1) by intercalating within the enzyme–DNA interface. Because the toxicity of these drugs depends on TOP1 trapping, cellular sensitivity to these compounds depends directly on TOP1 expression levels. As a result, the function of these drugs is to serve as enzyme poisons rather than inhibitors. This can be applied to treat tumor cells by utilizing TOP 2 enzyme poisons.[31]
References
- ^ Deans, AJ; West, SC (24 June 2011). "DNA interstrand crosslink repair and cancer". Nature Reviews. Cancer. 11 (7): 467–80. doi:10.1038/nrc3088. PMC 3560328. PMID 21701511.
- ^ Guainazzi, Angelo; Schärer, Orlando D. (2010-11-01). "Using synthetic DNA interstrand crosslinks to elucidate repair pathways and identify new therapeutic targets for cancer chemotherapy". Cellular and Molecular Life Sciences. 67 (21): 3683–3697. doi:10.1007/s00018-010-0492-6. ISSN 1420-682X. PMC 3732395. PMID 20730555.
- ^ Cancer, Cleveland Clinic. "Nitrogen Mustard – Chemotherapy Drugs – Chemocare". chemocare.com. Retrieved 2017-10-09.
- ^ Jamieson, E. R.; Lippard, S. J. (1999-09-08). "Structure, Recognition, and Processing of Cisplatin-DNA Adducts". Chemical Reviews. 99 (9): 2467–2498. doi:10.1021/cr980421n. ISSN 1520-6890. PMID 11749487.
- ^ Poklar N, Pilch DS, Lippard SJ, Redding EA, Dunham SU, Breslauer KJ (July 1996). "Influence of cisplatin intrastrand crosslinking on the conformation, thermal stability, and energetics of a 20-mer DNA duplex". Proc. Natl. Acad. Sci. U.S.A. 93 (15): 7606–11. Bibcode:1996PNAS...93.7606P. doi:10.1073/pnas.93.15.7606. PMC 38793. PMID 8755522.
- ^ Rudd GN, Hartley JA, Souhami RL (1995). "Persistence of cisplatin-induced DNA interstrand crosslinking in peripheral blood mononuclear cells from elderly and young individuals". Cancer Chemother. Pharmacol. 35 (4): 323–6. doi:10.1007/BF00689452. PMID 7828275. S2CID 24036376.
- ^ Coste, F.; Malinge, J. M.; Serre, L.; Shepard, W.; Roth, M.; Leng, M.; Zelwer, C. (1999-04-15). "Crystal structure of a double-stranded DNA containing a cisplatin interstrand cross-link at 1.63 A resolution: hydration at the platinated site". Nucleic Acids Research. 27 (8): 1837–1846. doi:10.1093/nar/27.8.1837. ISSN 0305-1048. PMC 148391. PMID 10101191.
- ^ "Cisplatin". National Cancer Institute. 2007-03-02. Retrieved 2017-10-09.
- ^ Cimino, G. D.; Gamper, H. B.; Isaacs, S. T.; Hearst, J. E. (1985). "Psoralens as photoactive probes of nucleic acid structure and function: organic chemistry, photochemistry, and biochemistry". Annual Review of Biochemistry. 54: 1151–1193. doi:10.1146/annurev.bi.54.070185.005443. ISSN 0066-4154. PMID 2411210. S2CID 21013934.
- ^ Qi Wu, Laura A Christensen, Randy J Legerski & Karen M Vasquez, Mismatch repair participates in error-free processing of DNA interstrand crosslinks in human cells,EMBO Reports 6, 6, 551–557 (2005).
- ^ Kirchner, James J.; Sigurdsson, Snorri T.; Hopkins, Paul B. (1992-05-01). "Interstrand cross-linking of duplex DNA by nitrous acid: covalent structure of the dG-to-dG cross-link at the sequence 5'-CG". Journal of the American Chemical Society. 114 (11): 4021–4027. doi:10.1021/ja00037a001. ISSN 0002-7863.
- ^ Stone, Michael P.; Cho, Young-Jin; Huang, Hai; Kim, Hye-Young; Kozekov, Ivan D.; Kozekova, Albena; Wang, Hao; Minko, Irina G.; Lloyd, R. Stephen (2008-07-01). "Interstrand DNA Cross-Links Induced by α,β-Unsaturated Aldehydes Derived from Lipid Peroxidation and Environmental Sources". Accounts of Chemical Research. 41 (7): 793–804. doi:10.1021/ar700246x. ISSN 0001-4842. PMC 2785109. PMID 18500830.
- ^ Niedernhofer, Laura J.; Daniels, J. Scott; Rouzer, Carol A.; Greene, Rachel E.; Marnett, Lawrence J. (2003-08-15). "Malondialdehyde, a Product of Lipid Peroxidation, Is Mutagenic in Human Cells". Journal of Biological Chemistry. 278 (33): 31426–31433. doi:10.1074/jbc.m212549200. ISSN 0021-9258. PMID 12775726.
- ^ Dooley, Patricia A.; Zhang, Mingzhou; Korbel, Gregory A.; Nechev, Lubomir V.; Harris, Constance M.; Stone, Michael P.; Harris, Thomas M. (2003-01-08). "NMR determination of the conformation of a trimethylene interstrand cross-link in an oligodeoxynucleotide duplex containing a 5'-d(GpC) motif". Journal of the American Chemical Society. 125 (1): 62–72. doi:10.1021/ja0207798. ISSN 0002-7863. PMID 12515507.
- ^ LC Colis; P Raychaudhury; AK Basu (2008). "Mutational specificity of gamma-radiation-induced guanine-thymine and thymine-guanine intrastrand cross-links in mammalian cells and translesion synthesis past the guanine-thymine lesion by human DNA polymerase eta". Biochemistry. 47 (6): 8070–8079. doi:10.1021/bi800529f. PMC 2646719. PMID 18616294.
- ^ Box, Harold C.; Budzinski, Edwin E.; Dawidzik, Jean D.; Wallace, John C.; Evans, Marianne S.; Gobey, Jason S. (1996). "Radiation-Induced Formation of a Crosslink between Base Moieties of Deoxyguanosine and Thymidine in Deoxygenated Solutions of d(CpGpTpA)". Radiation Research. 145 (5): 641–643. Bibcode:1996RadR..145..641B. doi:10.2307/3579285. JSTOR 3579285. PMID 8619032.
- ^ Klein Douwel, Daisy; Boonen, Rick A.C.M.; Long, David T.; Szypowska, Anna A.; Räschle, Markus; Walter, Johannes C.; Knipscheer, Puck (2014). "XPF-ERCC1 Acts in Unhooking DNA Interstrand Crosslinks in Cooperation with FANCD2 and FANCP/SLX4". Molecular Cell. 54 (3): 460–471. doi:10.1016/j.molcel.2014.03.015. PMC 5067070. PMID 24726325.
- ^ DNA repair and mutagenesis. Friedberg, Errol C., Friedberg, Errol C. (2nd ed.). Washington, D.C.: ASM Press. 2006. ISBN 9781555813192. OCLC 59360087.
{{cite book}}: CS1 maint: others (link) - ^ Admiraal, Suzanne J.; O’Brien, Patrick J. (2015-03-10). "Base Excision Repair Enzymes Protect Abasic Sites in Duplex DNA from Interstrand Cross-Links". Biochemistry. 54 (9): 1849–1857. doi:10.1021/bi501491z. ISSN 0006-2960. PMC 4404639. PMID 25679877.
- ^ Zhao, Linlin; Xu, Wenyan (2015-12-02). "Mutagenic Bypass of an Oxidized Abasic Lesion-Induced DNA Interstrand Cross-Link Analogue by Human Translesion Synthesis DNA Polymerases". Biochemistry. 54 (50): 7409–7422. doi:10.1021/acs.biochem.5b01027. PMC 4700817. PMID 26626537.
- ^ Zhao, Linlin; Xu, Wenyan (2016-10-21). "O6-2′-Deoxyguanosine-butylene-O6-2′-deoxyguanosine DNA Interstrand Cross-Links Are Replication-Blocking and Mutagenic DNA Lesions". Chem. Res. Toxicol. 29 (11): 1872–1882. doi:10.1021/acs.chemrestox.6b00278. PMC 5665164. PMID 27768841.
- ^ Cole RS, Levitan D, Sinden RR (1976). "Removal of psoralen interstrand cross-links from DNA of Escherichia coli: mechanism and genetic control". J. Mol. Biol. 103 (1): 39–59. doi:10.1016/0022-2836(76)90051-6. PMID 785009.
- ^ Sinden RR, Cole RS (1978). "Repair of cross-linked DNA and survival of Escherichia coli treated with psoralen and light: effects of mutations influencing genetic recombination and DNA metabolism". J. Bacteriol. 136 (2): 538–47. doi:10.1128/jb.136.2.538-547.1978. PMC 218577. PMID 361714.
- ^ Noll DM, Mason TM, Miller PS (2006). "Formation and repair of interstrand cross-links in DNA". Chem. Rev. 106 (2): 277–301. doi:10.1021/cr040478b. PMC 2505341. PMID 16464006.
- ^ Tretyakova, Natalia; Groehler, Arnold; Ji, Shaofei (2015). "DNA-Protein Cross-links: Formation, Structural Identities, and Biological Outcomes". Acc Chem Res. 48 (6): 1631–44. doi:10.1021/acs.accounts.5b00056. PMC 4704791. PMID 26032357.
- ^ Pendergrast, P.; Chen, Yan; Ebright, Yon; Ebright, Richard (1992). "Determination of the orientationof a DNA binding motif in a protein-DNA complex by photocrosslinking" (PDF). Proc. Natl. Acad. Sci. U.S.A. 89 (21): 10287–10291. Bibcode:1992PNAS...8910287P. doi:10.1073/pnas.89.21.10287. PMC 50323. PMID 1332042.
- ^ Smith, Kendric; Martin, Shetlar. "DNA-PROTEIN CROSSLINKS".
{{cite journal}}: Cite journal requires|journal=(help) - ^ Molina JR, Yang P, Cassivi SD, Schild SE, Adjei AA (2008). "Non-small cell lung cancer: epidemiology, risk factors, treatment, and survivorship". Mayo Clin. Proc. 83 (5): 584–94. doi:10.4065/83.5.584. PMC 2718421. PMID 18452692.
- ^ a b Taron M, Rosell R, Felip E, Mendez P, Souglakos J, Ronco MS, Queralt C, Majo J, Sanchez JM, Sanchez JJ, Maestre J (2004). "BRCA1 mRNA expression levels as an indicator of chemoresistance in lung cancer". Hum. Mol. Genet. 13 (20): 2443–9. doi:10.1093/hmg/ddh260. PMID 15317748.
- ^ a b Papadaki C, Sfakianaki M, Ioannidis G, Lagoudaki E, Trypaki M, Tryfonidis K, Mavroudis D, Stathopoulos E, Georgoulias V, Souglakos J (2012). "ERCC1 and BRAC1 mRNA expression levels in the primary tumor could predict the effectiveness of the second-line cisplatin-based chemotherapy in pretreated patients with metastatic non-small cell lung cancer". J Thorac Oncol. 7 (4): 663–71. doi:10.1097/JTO.0b013e318244bdd4. PMID 22425915.
- ^ Stingele, Julian; Bellelli, Roberto; Boulton, Simon (September 2017). "Mechanisms of DNA–protein crosslink repair". Nature Reviews Molecular Cell Biology. 18 (9): 563–573. doi:10.1038/nrm.2017.56. PMID 28655905. S2CID 9938335.
External links
- PDB: 1AIO – Interactive structure for cisplatin and DNA adduct formation
- PDB: 204D – Interactive structure for psoralen and crosslinked DNA
- Psoralen Ultraviolet A Light Treatment